定量分析的必要性和局限性
定量分析能把抽象概念转化为直观画面,在网络安全与公共议题中都能帮助我们避免“想当然”。然而,方法不当也可能制造数字幻觉,比如主观打分或只看统计量不看图形。本文结合风险评估、生育率案例和安斯库姆四重奏,讨论了定量分析的必要性与局限性,以及在实践中如何更稳妥地使用。
我刚进网络安全这行时,风险评估服务还比较盛行。报告里常见的一种“定量分析”做法是:对某个/类风险的资产、威胁和脆弱性分别赋 1–5 分,相乘得到 1–125 的风险值,再设一个阈值(比如 75),超过就判为高风险。
当时我觉得这种定量意义不大:不同人的赋分方差很大,缺少客观标尺;更关键的是,这类 1–5 分多半只是“排序意义”的分值,硬拿去做乘法会制造一种“精确的错觉”。很快,不只风险评估,整个“风险度量”在网安行业都失去了热度。
话说回来,基于数据的决策仍非常有价值。人脑很容易对抽象概念形成直觉判断,而这些判断常和数据相悖;当不经数据分析就对自己的想当然大谈特谈时,爹味和老登味就开始冒头了。为了避免这种“直觉暴走”,定量分析能把讨论拉回到证据层面。
举个例子。生育率是这几年的社会热点。大家都听过更替生育率 2.1:女性一生平均生育 2.1 个子女,才能大致维持人口规模稳定。问题是,“2.1 的社会”到底是什么画面?这时定量分析就有了用武之地。
以 36 人/班(ChatGPT告诉我的去年北京小学的平均每班人数)的常见班额做一个示意(不考虑双胞胎且同班就读、重组家庭等复杂因素):
如果班上 18 个学生是独生子女,18 个学生有一个兄弟姐妹,则这个班级群体的生育率是(18×1+18×2)/36=1.5,显然不够。
一个“达到 2.1” 的班级可能是这样的结构:10 个学生是独生子女,12 个有一个兄弟姐妹,14 个有两个兄弟姐妹。这时这个班级群体的生育率是(10×1+12×2+14×3)/36≈2.11
这还没有考虑不生育家庭和女性的情况,如果有 5% 具有生育能力的女性选择不生育,要想维持整体 2.1,需要这个班级有7个学生是独生子女,14个学生有一个兄弟姐妹,15个学生有二个兄弟姐妹。这时这个班级群体加上对应不生育群体的生育率才将将够(7*1+14*2+15*3)/ROUND(“36*1.05”,0)≈2.11。
也就是差不多1/5的独生子女,2/5的人有超过一个兄弟姐妹。不管是学校,还是补习班,只要是同龄人群体就需要满足这样的比例,整个群体的生育率才够2.1。
(这是为了建立直觉的简化示意,真实世界还会受到性别比、代际结构、婚育年龄等影响。)
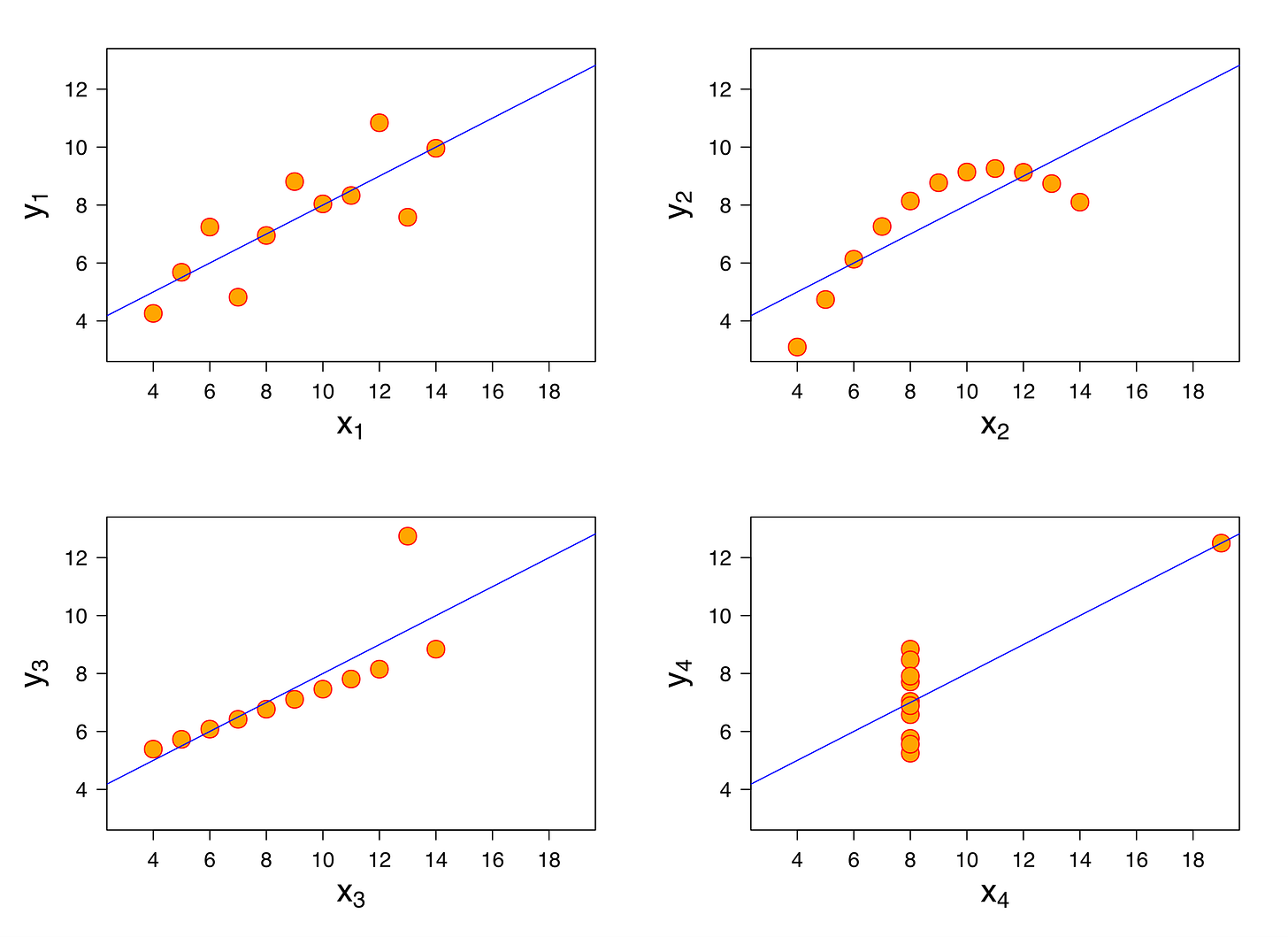
当然,定量分析也有它的局限。上面这组数据叫“安斯库姆四重奏”(Anscombe’s Quartet):它们是四组看起来完全不同的散点图,但在 x、y 的均值和方差、x 与 y 的相关系数、线性回归线等统计摘要却一模一样。如果只看统计结果不看图形,我们就会被数据“愚弄”。
所以,对定量分析我的看法是:它非常有力量,但必须贴着具体数据与问题本身来用。在网安这样的工程场景里,尽量减少主观打分的“乘法魔法”,明确口径,能用结果变量就用结果变量(比如用实际损失、处置效率、MTTR 等去做复盘);在不确定性不可避免时,用区间/误差条而不是一个点。这样,数字才不会变成装饰,而能真正帮助我们避免想当然。